6576. Road
In a certain country, there are n roads
numbered from 1 to n. A civil engineer must build a
public road network that connects all cities, meaning it must be possible to
travel from any city to any other, possibly via intermediate cities. His team
has surveyed several routes (roads between pairs of cities). Each road is
bidirectional. Building a road requires certain costs: the shorter the route,
the cheaper the construction.
The engineer has never planned a road network in advance. He simply
chooses a road he likes and builds it until all cities are connected.
Now the engineer wants to build a road between cities p and q.
Under pressure from the government, aiming to reduce expenses, he asks you to
write a program that determines whether it is worth building this road. Your
program should print “YES” if, after construction, the road (p, q) will
be part of the minimum road network connecting all cities. Otherwise, it should
print “NO”.
Input. The first line contains the number of
test cases t (t≤10).
Each test case begins with a line containing four integers n,
m, p, and q. Here n (2 ≤ n ≤
10000) is the number of cities, m (1 ≤ m ≤ 20000) is
the number of roads, and p and q (1 ≤ p, q ≤
n) specify the cities between which the engineer intends to build a
road.
The next m lines each contain three integers u, v, and
w (1 ≤ u, v ≤ n, 1 ≤ w ≤
4⋅105) describing
an existing bidirectional road of length w between cities u and v.
All road lengths are distinct. There can be at most one road between any pair
of cities. It is guaranteed that the graph is connected, i.e., there is a path
between any pair of cities. All numbers are integers.
Output. For each test case, print “YES” if the
road (p, q) will be part of the minimum road network.
Otherwise, print “NO”.
|
Sample input |
Sample output |
|
3 2 1 1 2 1 2 4 3 3 2 3 1 2 1 1 3 2 2 3 3 4 5 3 4 1 2 1 1 3 3 3 4 2 1 4 4 4 2 5 |
YES NO YES |
SOLUTION
graphs – Kruskal algorithm
Algorithm analysis
Run Kruskal’s algorithm on the initial graph. In the set
s, store the edges that belong to the minimum spanning tree. Next, check
whether the given edge (p, q) is part of this spanning tree. To
do this, we need to verify whether the pair (p, q) or (q, p)
is contained in the set s.
Example
The graphs
given in the examples have the following form:
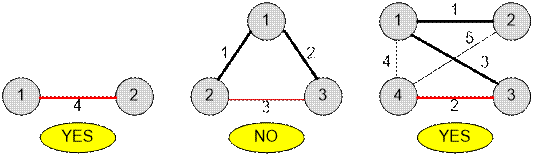
Algorithm implementation
Define a structure for a graph edge that contains a pair of vertices and
the edge weight. Define an array of edges e.
struct Edge
{
int u, v, dist;
};
vector<Edge> e;
Define an array parent, which is used to
implement the disjoint set union structure.
vector<int> parent;
The function Repr finds the representative
of the set to which vertex n belongs.
int Repr(int n)
{
while(n != parent[n]) n = parent[n];
return n;
}
The function Union merges the sets
containing the elements x and y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return 0;
parent[y] = x;
return 1;
}
The function lt serves as a comparator
for sorting the edges.
int lt(Edge a, Edge b)
{
return (a.dist <
b.dist);
}
The main part of the program. Process several test cases.
scanf("%d", &tests);
while (tests--)
{
Read the input data. Initialize the parent array.
scanf("%d
%d %d %d", &n, &m, &p, &q);
parent.resize(n
+ 1);
for (i = 1; i <= n; i++) parent[i] = i;
Read the graph edges.
e.resize(m);
for (i = 0; i
< m; i++)
scanf("%d
%d %d", &e[i].u, &e[i].v, &e[i].dist);
Sort the graph edges in ascending order of their weights.
sort(e.begin(),
e.end(), lt);
For each test case, reset the variable flag. It takes the value 1
or 0 depending on whether the edge (p, q) belongs to the minimum
spanning tree.
flag = 0;
Run Kruskal’s algorithm to construct the minimum spanning tree. If the
edge (e[i].u, e[i].v) is included in the
spanning tree, check whether it matches the edge (p, q).
for (i = 0; i
< m; i++)
if (Union(e[i].u, e[i].v))
It is necessary to check two conditions:
(e[i].u, e[i].v)
= (p, q) and (e[i].u,
e[i].v) = (q, p).
if ((e[i].u == p && e[i].v == q) ||
(e[i].u == q && e[i].v == p))
{
If the edge (e[i].u, e[i].v) matches (p, q) or (q, p), set flag = 1 and break the loop.
flag = 1;
break;
}
Depending on the value of the variable flag, print the answer.
if (flag)
puts("YES");
else
puts("NO");
}
Algorithm implementation – set
Define a structure for a graph edge that contains a pair of vertices and
the edge weight. Define an array of edges e.
struct Edge
{
int u, v, dist;
};
vector<Edge> e;
Define an array parent, which is used to
implement the disjoint set union structure.
vector<int> parent;
In the set s, store the edges that belong to the minimum spanning
tree.
set<pair<int, int> > s;
The function Repr finds the representative
of the set to which vertex n belongs.
int Repr(int n)
{
while(n != parent[n]) n = parent[n];
return n;
}
The function Union merges the sets
containing the elements x and y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return 0;
parent[y] = x;
return 1;
}
The function lt serves as a comparator
for sorting the edges.
int lt(Edge a, Edge b)
{
return (a.dist <
b.dist);
}
The main part of the program. Process several test cases.
scanf("%d", &tests);
while (tests--)
{
Read the input data. Initialize the parent array.
scanf("%d
%d %d %d", &n, &m, &p, &q);
parent.resize(n
+ 1);
for (i = 1; i <= n; i++) parent[i] = i;
Read the graph edges.
e.resize(m);
for (i = 0; i
< m; i++)
scanf("%d
%d %d", &e[i].u, &e[i].v, &e[i].dist);
Sort the graph edges in ascending order of their weights.
sort(e.begin(),
e.end(), lt);
For each test case, clear the set s.
s.clear();
Run Kruskal’s algorithm to construct the minimum spanning tree. If the
edge (e[i].u, e[i].v) is included in the
spanning tree, add it to the set s.
for (i = 0; i
< m; i++)
if
(Union(e[i].u, e[i].v)) s.insert(make_pair(e[i].u, e[i].v));
After the algorithm finishes, check whether the given
edge (p, q) belongs to the minimum spanning tree. To do this, we
need to determine whether the pair (p, q) or (q, p)
is contained in the set s.
if
((s.find(make_pair(p, q)) != s.end()) ||
(s.find(make_pair(q, p)) != s.end()))
puts("YES");
else
puts("NO");
}
Java implementation
import java.util.*;
class Edge
{
int u, v, dist;
Edge (int u, int v, int dist)
{
this.u = u;
this.v = v;
this.dist = dist;
}
};
class Pair
{
int u, v;
Pair (int u, int v)
{
this.u = u;
this.v = v;
}
};
public class Main
{
static int mas[];
static int size[];
static int Repr(int n)
{
if (n == mas[n]) return n;
return mas[n] = Repr(mas[n]);
}
static int Union(int x,int y)
{
x = Repr(x); y = Repr(y);
if(x == y) return 0;
if (size[x] < size[y])
{
int temp = x; x = y; y = temp;
}
mas[y] = x;
size[x] += size[y];
return 1;
}
public static class MyFun implements
Comparator<Edge>
{
public int
compare(Edge a, Edge b)
{
return a.dist - b.dist;
}
}
public static class PairFun implements
Comparator<Pair>
{
public int
compare(Pair a, Pair b)
{
if (a.u == b.u) return a.v - b.v;
return a.u - b.u;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int tests = con.nextInt();
while(tests-- > 0)
{
int n = con.nextInt();
int m = con.nextInt();
int p = con.nextInt();
int q = con.nextInt();
mas = new int[n+1];
size = new int[n+1];
for(int i = 1; i <= n; i++)
{
mas[i] = i;
size[i] = 1;
}
Vector<Edge> v = new
Vector<Edge>();
for(int i = 0; i < m; i++)
{
int x = con.nextInt();
int y = con.nextInt();
int dist = con.nextInt();
v.add(new Edge(x,y,dist));
}
Collections.sort(v, new MyFun());
TreeSet<Pair> s = new
TreeSet<Pair>(new PairFun());
for(int i = 0; i < m; i++)
if (Union(v.get(i).u,v.get(i).v) == 1) s.add(new Pair(v.get(i).u,v.get(i).v));
if(s.contains(new Pair(p,q)) || s.contains(new Pair(q,p)))
System.out.println("YES");
else
System.out.println("NO");
}
con.close();
}
}